Python program to find the rank of a matrix

The rank of a matrix is the maximum number of linearly independent rows or columns. In other words, we can say rank is the total number of non-zero rows in its row echelon form. Generally, it is denoted as rank(A) or rk(A) or sometimes rank A where A is the matrix name.

The rank of a null matrix will always be zero. Some examples of the finding rank of a matrix are given below.

Example 1:

Let A be the given matrix –

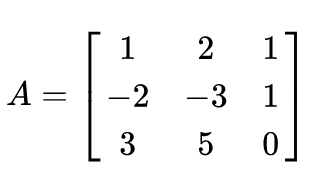
After performing a number of elementary row operations, the reduced row echelon form of the given matrix is –

As you can see in its reduced row echelon form there are two non-zero rows so the rank of matrix A will be 2.

Example 2:

Lets A is our matrix as it is given below –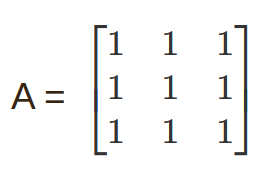After performing a number of elementary row operations the reduced row echelon form of the given matrix is –

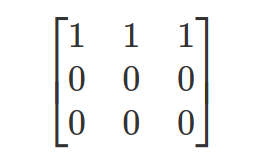
Here the number of non-zero rows is 1 thus the rank of the given matrix is 1.

Python program to find the rank of a matrix

To find the rank of a matrix in Python we will use linalg.matrix_rank()method of the NumPy library. This method returns the rank of the given matrix.

Before you import NumPy to your program make sure this package is installed on your system. Use the following command to install it –

sudo pip3 install numpy

Let’s see the program to find the rank of a matrix.

# Python program to find the rank of a matrix

import numpy as np

# Enter a mxn matrix
myMatrix = np.array([[1, 2, 1], [-2, -3, 1], [3, 5, 0]])
print("Given matrix is:")
for row in myMatrix:
    print(row)

# Finding the rank of the matrix
    rank = np.linalg.matrix_rank(myMatrix)
print("Rank of the given Matrix is : ",rank)

When you execute this program it will display the rank of the given matrix as you can see in the image below.

Another way to find the rank of a matrix is to find the reduced row echelon form of a matrix and then find its rank by observing the total number of non-zero rows in the matrix.